Hằng đẳng thức là một trong những công cụ quan trọng trong toán học, giúp giải quyết nhiều bài toán phức tạp và phát triển tư duy logic. Bài viết này sẽ giới thiệu 10 hằng đẳng thức quan trọng nhất mà mọi học sinh cần nắm vững.
Tầm Quan Trọng của Hằng Đẳng Thức
Vai Trò Trong Học Tập
Hằng đẳng thức đóng vai trò then chốt trong việc:
- Giải quyết các bài toán tối ưu
- Chứng minh các bất đẳng thức phức tạp
- Phát triển tư duy logic và khả năng suy luận
- Tạo nền tảng cho các môn học nâng cao

10 Hằng Đẳng Thức Cơ Bản
1. Hằng Đẳng Thức Bình Phương (Cauchy)
(a + b)² = a² + 2ab + b²
Đây là hằng đẳng thức cơ bản nhất, được sử dụng rộng rãi trong:
- Khai triển biểu thức
- Rút gọn đại số
- Giải phương trình bậc hai
2. Hằng Đẳng Thức Lập Phương
(a + b)³ = a³ + 3a²b + 3ab² + b³
Ứng dụng chính:
- Tính toán thể tích
- Giải các bài toán hình học không gian
- Phân tích đa thức
3. Bất Đẳng Thức Cauchy-Schwarz
(a₁² + a₂² + … + aₙ²)(b₁² + b₂² + … + bₙ²) ≥ (a₁b₁ + a₂b₂ + … + aₙbₙ)²
Ứng dụng trong:
- Hình học không gian
- Lý thuyết xác suất
- Giải tích nhiều biến
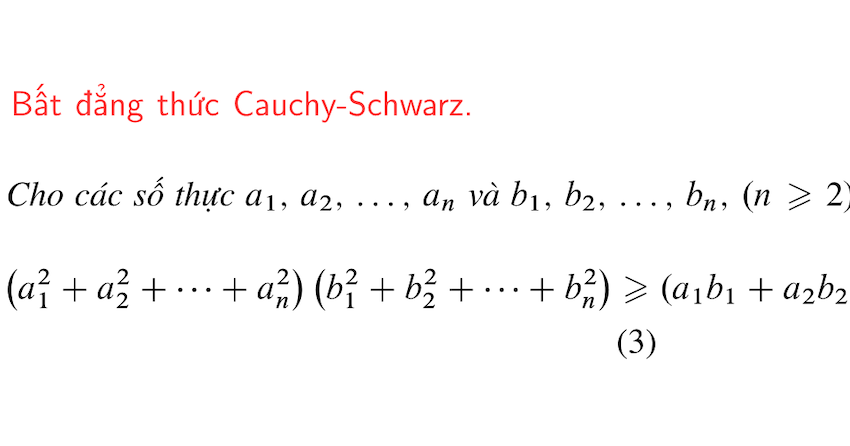
4. Bất Đẳng Thức Bernoulli
(1 + x)ⁿ ≥ 1 + nx (với n ≥ 1, x > -1)
Sử dụng cho:
- Chứng minh bất đẳng thức
- Tối ưu hóa
- Tính giới hạn
5. Bất Đẳng Thức Giữa Trung Bình
TB Cộng ≥ TB Nhân ≥ TB Điều Hòa
Áp dụng trong:
- Kinh tế học
- Thống kê
- Vật lý
Xem thêm Hằng Đẳng Thức Số 4: Giải Thích Chi Tiết Và Ứng Dụng Trong Toán Học
6. Hằng Đẳng Thức Tam Thức Bậc Hai
ax² + bx + c = a(x – x₁)(x – x₂)
Quan trọng trong:
- Giải phương trình bậc hai
- Khảo sát hàm số
- Tìm cực trị
7. Hằng Đẳng Thức Sophie Germain
(a⁴ + b⁴) ≥ 2(ab)²
Ứng dụng cho:
- Chứng minh phức tạp
- Bài toán tối ưu
- Lý thuyết số
8. Bất Đẳng Thức Jensen
f(λ₁x₁ + λ₂x₂ + … + λₙxₙ) ≤ λ₁f(x₁) + λ₂f(x₂) + … + λₙf(xₙ)
Sử dụng trong:
- Tối ưu hóa
- Lý thuyết xác suất
- Kinh tế học
9. Hằng Đẳng Thức Vieta
x₁ + x₂ = -b/a x₁x₂ = c/a
Áp dụng cho:
- Giải phương trình
- Tìm quan hệ giữa nghiệm
- Chứng minh đại số
Xem thêm Tổng hợp các hằng đẳng thức mở rộng cơ bản và nâng cao: Chìa khóa giải nhanh Toán học
10. Bất Đẳng Thức Tam Giác
|a – b| ≤ |a| + |b|
Quan trọng trong:
- Hình học
- Giải tích
- Số học
Phương Pháp Học Tập Hiệu Quả
Chiến Lược Ghi Nhớ
- Phân loại hằng đẳng thức:
- Theo mức độ khó
- Theo lĩnh vực ứng dụng
- Theo quan hệ logic
- Thực hành thường xuyên:
- Làm bài tập đa dạng
- Tự tạo bài tập mới
- Giải thích cho người khác

Tránh Sai Lầm Phổ Biến
- Điều kiện áp dụng:
- Kiểm tra miền xác định
- Xét các trường hợp đặc biệt
- Chú ý điều kiện biên
- Kỹ thuật chứng minh:
- Chứng minh trực tiếp
- Chứng minh phản chứng
- Quy nạp toán học
Ứng Dụng Thực Tiễn
Trong Học Tập
- Giải toán:
- Rút gọn phép tính
- Tìm giá trị lớn nhất, nhỏ nhất
- Chứng minh bất đẳng thức
- Nghiên cứu khoa học:
- Phân tích dữ liệu
- Tối ưu hóa quy trình
- Mô hình hóa vấn đề
Trong Đời Sống
- Kinh tế:
- Tính toán lãi suất
- Phân tích đầu tư
- Tối ưu chi phí
- Kỹ thuật:
- Thiết kế công trình
- Tính toán độ bền
- Tối ưu hiệu suất

Tài Liệu Tham Khảo và Hỗ Trợ
Nguồn Học Tập
- Tạp Chí Cha Mẹ (tapchichame.com):
- Bài giảng video
- Tài liệu PDF
- Bài tập tương tác
- Sách tham khảo:
- Sách giáo khoa
- Sách bài tập
- Sách chuyên đề
Kênh Hỗ Trợ
Để được hỗ trợ thêm, quý phụ huynh và học sinh có thể liên hệ:
- Hotline: 0907 07 07 07
- Email: [email protected]
- Website: tapchichame.com
Kết Luận
10 hằng đẳng thức trên đóng vai trò nền tảng trong toán học, giúp học sinh:
- Phát triển tư duy logic
- Nâng cao khả năng giải quyết vấn đề
- Tạo cơ sở cho việc học tập nâng cao
Việc nắm vững các hằng đẳng thức này không chỉ giúp cải thiện kết quả học tập mà còn phát triển tư duy toán học toàn diện. Hãy truy cập tapchichame.com để tìm hiểu thêm nhiều bài viết bổ ích khác về phương pháp học toán hiệu quả.
Bài viết được đăng tải trên Tạp Chí Cha Mẹ – Người bạn đồng hành tin cậy trong hành trình giáo dục con trẻ.
Thông tin liên hệ:
- Hotline: 0907 07 07 07
- Email: [email protected]
- Website: tapchichame.com
