Hằng đẳng thức là một chủ đề quan trọng trong chương trình toán học phổ thông và nâng cao. Bài viết này sẽ giúp học sinh và phụ huynh nắm vững các dạng bài tập về hằng đẳng thức cùng phương pháp giải chi tiết.

Các dạng bài tập cơ bản

Dạng 1: Chứng minh hằng đẳng thức đơn giản

Ví dụ 1: Chứng minh rằng với mọi số thực a, b ta có: (a + b)² = a² + 2ab + b²

Hướng dẫn giải:

1. Khai triển vế trái: (a + b)(a + b)
2. Áp dụng phép nhân đa thức: a × a + a × b + b × a + b × b
3. Rút gọn: a² + 2ab + b²

Ví dụ 2: Chứng minh rằng: (a – b)² + (b – c)² + (c – a)² = 2(a² + b² + c² – ab – bc – ca)

Hướng dẫn giải:

1. Khai triển vế trái:
   • (a – b)² = a² + b² – 2ab
   • (b – c)² = b² + c² – 2bc
   • (c – a)² = c² + a² – 2ca
2. Cộng các biểu thức
3. Rút gọn và so sánh hai vế

Dạng 2: Tính giá trị biểu thức

Ví dụ 3: Tính giá trị của biểu thức P = (x + 2)(x + 3) – (x + 1)(x + 4) với x = 1

Hướng dẫn giải:

1. Thay x = 1 vào biểu thức
2. Tính từng nhóm trong ngoặc
3. Thực hiện phép trừ để có kết quả cuối cùng

Xem thêm 10 Hằng Đẳng Thức Đáng Nhớ Trong Toán Học

Các dạng bài tập trung bình

Dạng 3: Chứng minh bất đẳng thức

Ví dụ 4: Chứng minh rằng với mọi số thực dương a, b ta có: (a + b)/2 ≥ √(ab)

Hướng dẫn giải:

1. Đặt (a – b)² ≥ 0 (vì bình phương luôn không âm)
2. Khai triển: a² – 2ab + b² ≥ 0
3. Cộng 4ab vào hai vế: a² + 2ab + b² ≥ 4ab
4. (a + b)² ≥ 4ab
5. a + b ≥ 2√(ab)
6. (a + b)/2 ≥ √(ab)

Dạng 4: Tìm giá trị lớn nhất, nhỏ nhất

Ví dụ 5: Tìm giá trị nhỏ nhất của biểu thức P = x² + 1/x² với x > 0

Hướng dẫn giải:

1. Áp dụng bất đẳng thức Cauchy: x² + 1/x² ≥ 2√(x² × 1/x²) = 2
2. Dấu “=” xảy ra khi x² = 1/x², tức là x = 1
3. Vậy giá trị nhỏ nhất của P là 2, đạt được khi x = 1

Các dạng bài tập nâng cao

Dạng 5: Chứng minh hằng đẳng thức có tham số

Ví dụ 6: Cho a, b, c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng:

(a²/b) + (b²/c) + (c²/a) ≥ a + b + c = 1

Hướng dẫn giải:

1. Áp dụng bất đẳng thức Cauchy cho từng cặp số
2. Kết hợp với điều kiện a + b + c = 1
3. Sử dụng phương pháp quy nạp hoặc biến đổi đại số

Xem thêm Hằng Đẳng Thức Số 4: Giải Thích Chi Tiết Và Ứng Dụng Trong Toán Học

Dạng 6: Tìm điều kiện của tham số

Ví dụ 7: Tìm các giá trị của tham số m để hằng đẳng thức sau đúng với mọi x:

mx² + (m+1)x + 1 = (x + 1)²

Hướng dẫn giải:

1. Khai triển vế phải: x² + 2x + 1
2. So sánh hệ số của hai vế
3. Lập hệ phương trình và giải

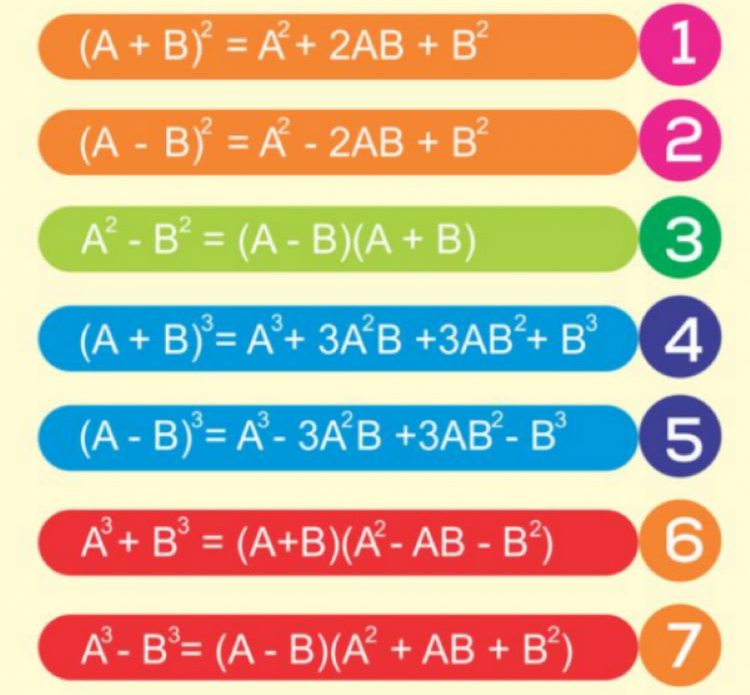
Phương pháp giải các bài tập khó

Các chiến thuật chứng minh

1. Phương pháp đại số:
   • Khai triển biểu thức
   • Phân tích thành nhân tử
   • Nhóm các số hạng tương tự
2. Phương pháp quy nạp:
   • Chứng minh đúng với n = 1
   • Giả sử đúng với n = k
   • Chứng minh đúng với n = k + 1
3. Phương pháp phản chứng:
   • Giả sử kết luận sai
   • Tìm mâu thuẫn
   • Kết luận mệnh đề đúng

Xem thêm Tổng hợp các hằng đẳng thức mở rộng cơ bản và nâng cao: Chìa khóa giải nhanh Toán học

Các kỹ thuật giải nâng cao

1. Kỹ thuật ước lượng:
   • Sử dụng các bất đẳng thức cơ bản
   • Áp dụng các hằng đẳng thức đã biết
   • Tìm cận trên, cận dưới
2. Kỹ thuật biến đổi tương đương:
   • Biến đổi về dạng quen thuộc
   • Đưa về dạng có thể áp dụng công thức
   • Kiểm tra điều kiện tương đương

Bài tập tự luyện

Bài tập mức độ cơ bản

1. Chứng minh rằng: (a + b)³ = a³ + 3a²b + 3ab² + b³
2. Tính giá trị của biểu thức: P = (x – 1)(x + 2) – (x + 1)(x – 2) với x = 3
3. Chứng minh rằng với mọi số thực a, b: (a + b)² ≥ 4ab

Bài tập mức độ nâng cao

1. Chứng minh rằng với mọi số thực dương a, b, c:

a/(b+c) + b/(c+a) + c/(a+b) ≥ 3/2

2. Tìm giá trị nhỏ nhất của biểu thức:

P = x⁴ + 1/x⁴ với x > 0

3. Cho a, b, c là các số thực dương thỏa mãn a + b + c = 3. Chứng minh rằng:

a² + b² + c² ≥ 3

Lời khuyên và phương pháp học tập

Cách tiếp cận bài tập

1. Đọc kỹ đề bài và xác định yêu cầu
2. Phân tích các điều kiện đã cho
3. Chọn phương pháp giải phù hợp
4. Thực hiện giải từng bước
5. Kiểm tra lại kết quả

Phương pháp rèn luyện

1. Luyện tập thường xuyên
2. Bắt đầu từ bài tập đơn giản
3. Tăng dần độ khó
4. Ghi chép và tổng kết phương pháp
5. Học hỏi từ lời giải mẫu

Kết luận

Việc nắm vững các dạng bài tập về hằng đẳng thức không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn phát triển tư duy logic và khả năng giải quyết vấn đề. Để thành công, các em cần:

1. Hiểu rõ lý thuyết cơ bản
2. Thực hành nhiều bài tập
3. Học cách vận dụng linh hoạt
4. Rèn luyện tư duy sáng tạo

Thông tin liên hệ

Để được tư vấn thêm về phương pháp học tập và các khóa học toán nâng cao, quý phụ huynh và học sinh vui lòng liên hệ:

• Hotline: 0907 07 07 07
• Email: [email protected]
• Website: tapchichame.com

Bài viết được đăng tải trên Tạp Chí Cha Mẹ – Nguồn tài liệu đáng tin cậy cho việc học tập và rèn luyện của học sinh.