Hằng đẳng thức là một trong những công cụ quan trọng trong việc giải toán, đặc biệt là trong các bài toán Olympic và các kỳ thi chuyên. Bài viết này sẽ giúp các bạn học sinh và phụ huynh hiểu rõ hơn về các hằng đẳng thức nâng cao thường gặp và cách áp dụng chúng.
Các hằng đẳng thức cơ bản và nâng cao
Nhắc lại các hằng đẳng thức cơ bản
Trước khi đi vào các hằng đẳng thức nâng cao, chúng ta cần nhớ lại một số hằng đẳng thức cơ bản:
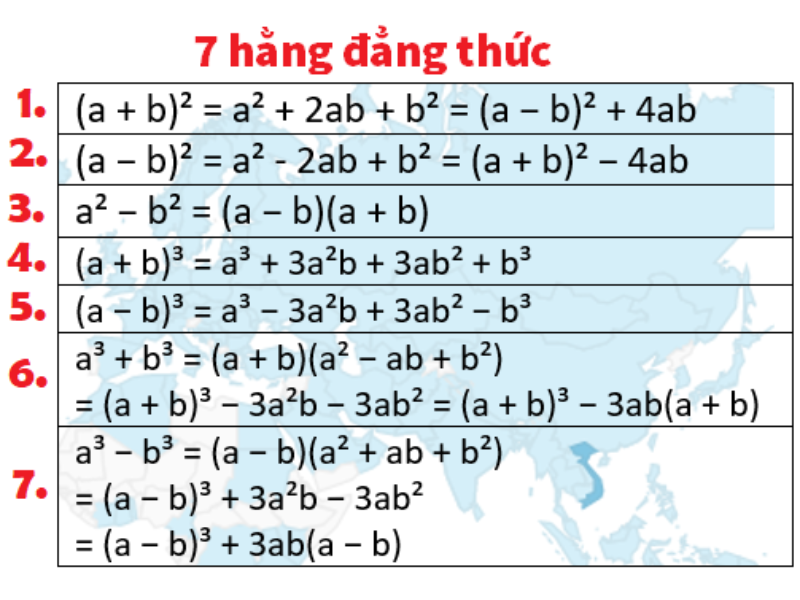
- Bình phương của tổng: (a + b)² = a² + 2ab + b²
- Bình phương của hiệu: (a – b)² = a² – 2ab + b²
- Hiệu bình phương: a² – b² = (a + b)(a – b)
- Lập phương của tổng: (a + b)³ = a³ + 3a²b + 3ab² + b³
- Lập phương của hiệu: (a – b)³ = a³ – 3a²b + 3ab² – b³
Các hằng đẳng thức nâng cao quan trọng
1. Hằng đẳng thức Cauchy
Đây là một trong những hằng đẳng thức quan trọng nhất:
- Với mọi số thực dương a, b ta có: (a + b)/2 ≥ √(ab)
- Dấu “=” xảy ra khi và chỉ khi a = b
2. Hằng đẳng thức Bernoulli
Với mọi x > -1, n ≥ 1, ta có:
- (1 + x)ⁿ ≥ 1 + nx
- Dấu “=” xảy ra khi x = 0 hoặc n = 1
Xem thêm Hiện Tại Phân Từ (Present Participle): Hướng Dẫn Toàn Diện Và Cách Sử Dụng
Các dạng hằng đẳng thức đặc biệt
Hằng đẳng thức liên quan đến ba biến
1. Hằng đẳng thức Nesbitt
Với mọi số thực dương a, b, c, ta có:
(a/(b+c) + b/(c+a) + c/(a+b)) ≥ 3/2Dấu “=” xảy ra khi và chỉ khi a = b = c
2. Bất đẳng thức AG-GM-HM
Với các số thực dương a₁, a₂, …, aₙ:
(a₁ + a₂ + ... + aₙ)/n ≥ ⁿ√(a₁×a₂×...×aₙ) ≥ n/(1/a₁ + 1/a₂ + ... + 1/aₙ)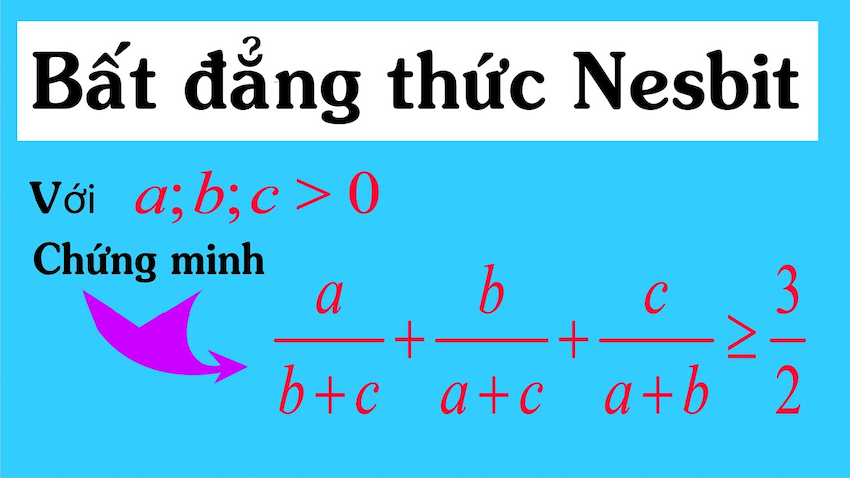
Hằng đẳng thức trong hình học
1. Hằng đẳng thức liên quan đến tam giác
- Định lý cosin: a² = b² + c² – 2bc×cosA
- Định lý sin: a/sinA = b/sinB = c/sinC = 2R (R là bán kính đường tròn ngoại tiếp)
2. Bất đẳng thức trong tam giác
- Bất đẳng thức tam giác: a + b > c
- Bất đẳng thức giữa các cạnh và góc: Cạnh lớn thì đối diện với góc lớn
Phương pháp chứng minh hằng đẳng thức
Các phương pháp chứng minh cơ bản
- Phương pháp biến đổi đại số:
- Chuyển vế
- Phân tích thành nhân tử
- Khai triển
- Nhóm các số hạng
- Phương pháp dùng bất đẳng thức cơ bản:
- Bất đẳng thức Cauchy
- Bất đẳng thức Bunhiacopxki
- Bất đẳng thức Jensen
Xem thêm Từ Vựng Tiếng Anh Cơ Bản Cho Người Mất Gốc – Phương Pháp Học Hiệu Quả Từ Con Số 0
Các kỹ thuật chứng minh nâng cao
- Phương pháp quy nạp:
- Chứng minh cho n = 1
- Giả sử đúng với n = k
- Chứng minh đúng với n = k + 1
- Phương pháp phản chứng:
- Giả sử điều cần chứng minh là sai
- Tìm ra mâu thuẫn
- Kết luận điều cần chứng minh là đúng

Ứng dụng trong giải toán
Bài toán về cực trị
1. Tìm cực trị không dùng đạo hàm
Sử dụng các hằng đẳng thức để tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
Ví dụ: Tìm giá trị nhỏ nhất của x² + 1/x² với x > 0
Giải: Áp dụng bất đẳng thức Cauchy: x² + 1/x² ≥ 2√(x²×1/x²) = 22. Bài toán tối ưu
Ứng dụng hằng đẳng thức trong các bài toán tối ưu:
- Tìm giá trị lớn nhất, nhỏ nhất
- Tìm kích thước tối ưu
- Tìm điều kiện tối ưu
Bài toán về chứng minh
1. Chứng minh bất đẳng thức
Các bước chứng minh:
- Phân tích bài toán
- Chọn phương pháp phù hợp
- Thực hiện chứng minh
- Kiểm tra dấu “=”
2. Chứng minh đẳng thức
Phương pháp chứng minh:
- Biến đổi về hai vế bằng nhau
- Sử dụng các hằng đẳng thức đã biết
- Kết hợp nhiều phương pháp

Luyện tập và ứng dụng
Các dạng bài tập thường gặp
- Bài tập về chứng minh bất đẳng thức:
- Sử dụng hằng đẳng thức Cauchy
- Áp dụng bất đẳng thức AM-GM
- Kết hợp nhiều bất đẳng thức
- Bài tập về tìm cực trị:
- Tìm giá trị lớn nhất, nhỏ nhất
- Chứng minh giá trị cực trị
- Tìm điều kiện đạt cực trị
Xem thêm Câu bị động kép trong tiếng Anh: Hướng dẫn toàn diện cho phụ huynh dạy con
Phương pháp giải các bài toán khó
- Chiến thuật giải bài toán phức tạp:
- Chia nhỏ bài toán
- Kết hợp nhiều phương pháp
- Tìm các mối liên hệ
- Lời khuyên khi giải toán:
- Đọc kỹ đề bài
- Xác định phương pháp phù hợp
- Kiểm tra lại kết quả
Kết luận và lời khuyên
Việc nắm vững các hằng đẳng thức nâng cao không chỉ giúp học sinh giải được các bài toán khó mà còn phát triển tư duy logic và khả năng phân tích vấn đề. Để học tốt phần này, các em cần:
- Nắm chắc kiến thức cơ bản
- Luyện tập thường xuyên
- Học cách vận dụng linh hoạt
- Tích lũy kinh nghiệm qua các bài tập
Thông tin liên hệ
Để được tư vấn thêm về phương pháp học tập và các khóa học toán nâng cao, quý phụ huynh và học sinh vui lòng liên hệ:
- Hotline: 0907 07 07 07
- Email: [email protected]
- Website: tapchichame.com
Bài viết được đăng tải trên Tạp Chí Cha Mẹ – Người bạn đồng hành tin cậy trong việc định hướng và phát triển năng lực học tập của con em.
