Trong toán học, việc tìm giá trị cực tiểu của một hàm số là một kỹ năng quan trọng, có nhiều ứng dụng trong thực tế. Tạp Chí Cha Mẹ sẽ giúp các bạn hiểu rõ về khái niệm này cùng các phương pháp xác định giá trị cực tiểu hiệu quả.
I. Khái niệm cơ bản về giá trị cực tiểu
1. Định nghĩa giá trị cực tiểu
Giá trị cực tiểu của một hàm số là giá trị nhỏ nhất của hàm số tại một điểm nào đó trong miền xác định. Tại điểm này, giá trị hàm số nhỏ hơn các giá trị lân cận của nó.

2. Phân biệt giá trị cực tiểu và giá trị nhỏ nhất
- Giá trị cực tiểu: Là giá trị nhỏ nhất cục bộ trong một khoảng nào đó
- Giá trị nhỏ nhất: Là giá trị nhỏ nhất trong toàn bộ miền xác định của hàm số
3. Điều kiện tồn tại giá trị cực tiểu
- Hàm số phải liên tục tại điểm đang xét
- Đạo hàm của hàm số phải tồn tại tại điểm đó
- Đạo hàm phải đổi dấu từ âm sang dương tại điểm đó
II. Các phương pháp tìm giá trị cực tiểu
1. Phương pháp dùng đạo hàm
Bước 1: Tìm đạo hàm của hàm số Bước 2: Giải phương trình đạo hàm bằng 0 Bước 3: Kiểm tra sự đổi dấu của đạo hàm Bước 4: Tính giá trị hàm số tại các điểm tìm được
2. Phương pháp dùng bất đẳng thức
- Sử dụng bất đẳng thức Cauchy
- Áp dụng bất đẳng thức AM-GM
- Sử dụng bất đẳng thức Bunhiacopxki
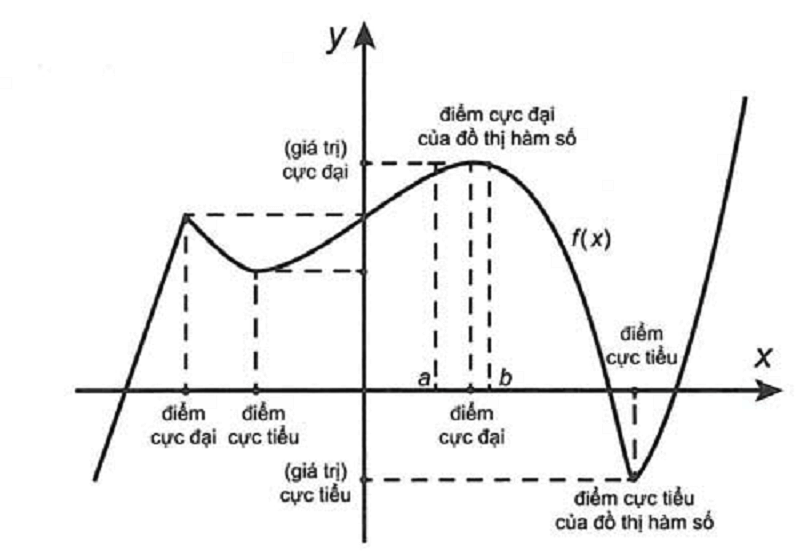
3. Phương pháp hình học
- Xác định ý nghĩa hình học của bài toán
- Sử dụng các tính chất hình học để tìm giá trị cực tiểu
III. Các dạng bài tập thường gặp
1. Tìm giá trị cực tiểu của biểu thức hai biến
Ví dụ 1: Tìm giá trị cực tiểu của biểu thức P = x² + y², biết x + y = 1
Lời giải:
- Đặt y = 1 – x
- P = x² + (1-x)² = 2x² – 2x + 1
- P’ = 4x – 2
- P’ = 0 ⟹ x = 1/2
- y = 1/2
- Giá trị cực tiểu là P(1/2) = 1/2
Xem thêm Cách giải phương trình bậc 3 nhanh chóng và hiệu quả
2. Tìm giá trị cực tiểu của biểu thức ba biến
Ví dụ 2: Tìm giá trị cực tiểu của P = x² + y² + z², biết x + y + z = 1
Lời giải:
- Áp dụng bất đẳng thức Cauchy: (x² + y² + z²)(1² + 1² + 1²) ≥ (x + y + z)²
- x² + y² + z² ≥ 1/3
- Dấu “=” xảy ra khi x = y = z = 1/3
- Vậy giá trị cực tiểu là 1/3

IV. Ứng dụng trong thực tế
1. Trong kinh tế
- Tối ưu hóa chi phí sản xuất
- Tìm điểm hòa vốn
- Xác định lợi nhuận tối đa
2. Trong kỹ thuật
- Thiết kế tối ưu
- Tính toán vật liệu
- Quy hoạch không gian
Xem thêm Tổng hợp các hằng đẳng thức mở rộng cơ bản và nâng cao: Chìa khóa giải nhanh Toán học
3. Trong khoa học tự nhiên
- Tìm quỹ đạo tối ưu
- Xác định điểm cân bằng
- Tính toán năng lượng tối thiểu
V. Phương pháp giải nâng cao
1. Phương pháp Lagrange
- Lập hàm Lagrange L(x,y,λ) = f(x,y) + λg(x,y)
- Tìm đạo hàm riêng theo x, y và λ
- Giải hệ phương trình thu được

2. Phương pháp vector
- Chuyển bài toán về dạng vector
- Sử dụng tích vô hướng
- Áp dụng bất đẳng thức Cauchy-Schwarz
VI. Bài tập tổng hợp
1. Bài tập cơ bản
- Tìm giá trị cực tiểu của P = x² + y², biết x + 2y = 2
- Tìm giá trị cực tiểu của P = x² + y² + z², biết x + y + z = 0
- Tìm giá trị cực tiểu của P = sinx + cosy, biết x + y = π/2
2. Bài tập nâng cao
- Tìm giá trị cực tiểu của P = x⁴ + y⁴, biết x² + y² = 2
- Tìm giá trị cực tiểu của P = x² + y² + z², biết x + y + z = 1 và xy + yz + zx = 0
Lời kết
Việc nắm vững phương pháp tìm giá trị cực tiểu không chỉ giúp học sinh giải được các bài toán khó mà còn phát triển tư duy logic và khả năng phân tích vấn đề. Hãy thường xuyên luyện tập với nhiều dạng bài tập khác nhau để cải thiện kỹ năng này.
Để được tư vấn thêm về phương pháp học toán hiệu quả và nhận thêm tài liệu học tập, quý phụ huynh và học sinh vui lòng liên hệ:
Tạp Chí Cha Mẹ
- Hotline: 0907 07 07 07
- Email: [email protected]
- Website: tapchichame.com
Chúc các bạn học tập tốt và đạt kết quả cao!
